DYNAMICAL SYSTEMS, ANOSOV FLOWS AND ARNOLD’S CAT PART 1

READERS OF THIS WEBSITE have been exposed occasionally to the mathematical concept of dynamical systems theory, what I have called “differential equations, sorta, without the dirty bits.” My own 15 minutes of fame amidst this came 2:40-2:55 p.m., January 29, 1975, in Predator/Prey Dynamics with Age Distribution, a joint paper that colleague Bill MacLean was kind enough to have me present at the Ninth Annual Symposium on Some Mathematical Questions in Biology, New York City, New York.

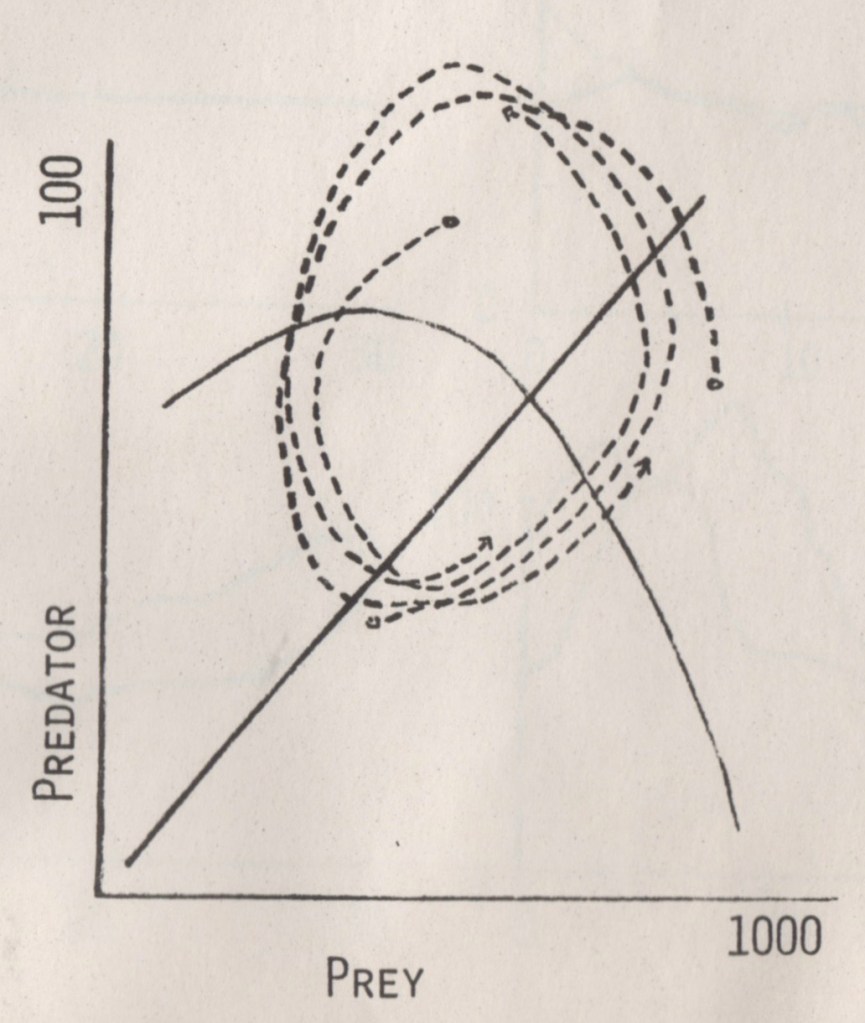
From time to time, I have read about advances in dynamical systems theory since then. In particular, Jordana Cepelewicz offers a fascination article “Flow Proof Helps Mathematicians Find Stability in Chaos” in Quanta magazine, June 15, 2023. Here, in Parts 1 and 2 today and tomorrow, are tidbits gleaned from this article and from my usual Internet sleuthing.

Cepelewicz begins by describing the meeting of Cornell’s Kathryn Mann, who “does research at the intersection of topology, dynamics and group theory,” and Queen’s University’s Thomas Barthelmé, “working on involving mathematical models called dynamical systems.”

Cepelewicz recounts, “ ‘We were just sitting in this coffee shop, drawing pictures, each of us trying to figure out what the other was trying to say,’ Mann said. ‘At the beginning, I was like, this guy makes no sense.’ But as they learned to speak each other’s mathematical languages, both became more optimistic about their chances of finding a solution.”

Chaos and Stability. Cepelewicz writes, “Barthelmé was interested in particular dynamical systems called Anosov flows, which crop up naturally in many areas of mathematics and act as important toy models. These systems showcase seemingly paradoxical properties all in one place: chaos and stability; rigidity and flexibility; the presence of intrinsic geometric structure amid an underlying topological wilderness.”

Dmitri Anosov was a Soviet mathematician. An Anosov Diffeomorphism is described briefly by Wikipedia as a special kind of mapping from a topological space to itself, one with “clearly marked local directions of ‘expansion’ and ‘contraction.’ ”

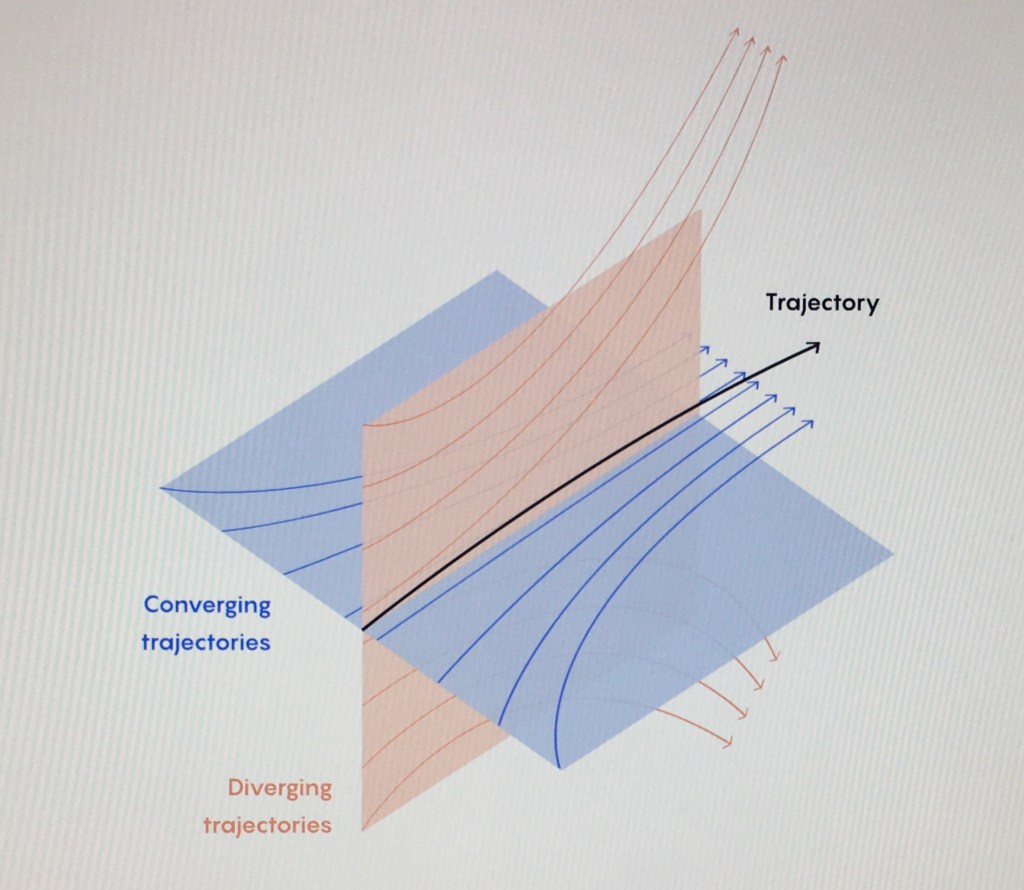
Mann is quoted: “In dynamics, you’re really interested in this confluence of stability and chaos.” Cepelewicz continues, “Anosov discovered that both chaos and stability arise automatically in a geodesic flow because its trajectories converge and diverge like lines drawn on a piece of taffy as it is squeezed together and stretched out.”

Fruit Flies to Humans; Anosov Flows to Other Dynamical Systems. Cepelewicz presents an analogy: “Just as scientists might try to learn about gene expression in a fruit fly before moving on to humans, mathematicians have proved results about topological, statistical and other properties in Anosov flows and then extended that work to other dynamical systems. For example, in the 1970s, mathematicians used what they knew about Anosov flows (and related systems) to formulate a conjecture about what kinds of flows can exhibit structural stability.” That is, how well a system reacts to perturbation.

As noted back in SimanaitisSays, November 15, 2014, “… if you haven’t figured this out already, life isn’t structurally stable.” But many dynamical systems are. Tomorrow in Part 2, we’ll meet Arnold’s Cat, a doppelganger for my pal ∏wacket. ds

© Dennis Simanaitis, SimanaitisSays.com, 2023